听说你至今不晓得缓存淘汰算法？实现LRU、LFU和FIFO？

前言

我们有一个自制的浏览器程序，现在需要对所有浏览过的页面数据进行缓存，如果页面已经被存储过则直接将数据拿出来进行页面的数据填充来提升访问性能，但是我们的程序是不可能为这部分缓存提供无限大的内存空间，而是要分配一个固定的最大空间来专门做这部分事情。因为这个空间大小的限制，若新访问的页面数据需要存入内存时发现内存空间已经满了，此时我们希望能够删除一些历史缓存数据，从而使新的访问数据可以被存储，此时删除什么样子的缓存数据就成了我们首先需要考虑问题。

一般我们认为，在当前自身业务场景下，淘汰算法中，缓存波动最小，命中率最高，运行性能最好的实现方式就是我们需要的的最优解，所以没有最优，只有最合适！

最优算法：OPT

由Belady在1966年提出的理念：优先淘汰以后不会被访问或者最迟才需要被访问的页面，它能保证我们的未来的命中率最高。但现实是很残酷的，这个方法需要我们去预测未来的操作，大部分情况下，未来是无规律可循，是无法预知的，因此也是无法被实现的。但它依然有被存在的意义：那就是为实现算法对性能进行衡量比较。

先进先出：FIFO

FIFO是所有算法中最容易理解也是最好实现的一种，它的本质就是清除最先进入内存的数据：因为最先进入内存的数据，其不再被使用的可能性比刚进入内存的数据可能性大，也因为这个特性，其在大多数的应用场景下效率不高，命中率比较低，因此使用频率非常低

实现原理：我们通过队列的方式来存储数据，新数据先检测队列内是否有对应的存储，如果有则不做处理，否则插入到队列的末尾，如果在插入时发现队列已经满了，则先删除队列头的数据，在将新数据插入到队列尾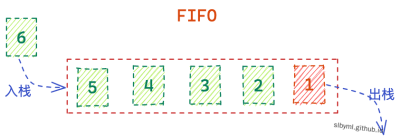

Array：[1,2,3,4,2,5,1,2,4,3]；size：3

class FIFOCaches {
  private caches:number[] = []
  private limit:number = 3
  has(cache:number):boolean {
    return this.caches.indexOf(cache) >= 0
  }
  getCaches():number[] {
    return this.caches
  }
  set(cache:number):void {
    const isCache = this.has(cache)
    if (isCache) return;
    if (this.caches.length >= this.limit) this.caches.shift();
    this.caches.push(cache)
  }
}
// test
var arr = [1,2,3,4,2,5,1,2,4,3]
const fifo = new FIFOCaches()
arr.forEach(item => fifo.set(item))
console.log(fifo.getCaches()) // [ 2, 4, 3 ]

代码输出如下：

访问	in：1	in：2	in：3	in：4	in：2	in：5	in：1	in：2	in：4	in：3
存储	1	1	1	2	2	3	4	5	1	2
存储		2	2	3	3	4	5	1	2	4
存储			3	4	4	5	1	2	4	3
命中	✗	✗	✗	✗	✓	✗	✗	✗	✗	✗

最少使用：LFU

LFU 是 Least Frequently Used 的缩写，也就是优先删除使用频率最低的数据，因为一般我们认为在当前阶段访问次数最少的数据，在未来也是一样的。因此它和数据被访问的次数是息息相关的。

存在的问题：存在缓存末端抖动；旧的热点数据因为其基数比较高，所以不容被清除。而新的热点数据存储因为其频次基数还比较低，所以总是容易被淘汰。

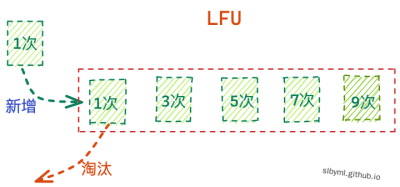
Array：[1,2,3,4,2,5,1,2,4,3]；size：3

interface Icache {
  value: number,
  freq: number
}
class LFUCache {
  private caches:Map<number, Icache>=new Map()
  private limit:number = 3
   getCaches():Map<number, Icache> {
    return this.caches
  }
   set(cache:number):void {
    const _cache = this.caches.get(cache)
    if (_cache) { // 有则更新命中次数
      _cache.freq++
      this.caches.set(cache, _cache)
    } else {
      if(this.caches.size >= this.limit){ // 存储超长则删除使用次数最少的cache
        let minFreqKey = this.caches.keys().next().value
        this.caches.forEach((item, key) => {
          minFreqKey = (this.caches.get(minFreqKey) as Icache).freq > item.freq ? key : minFreqKey
        })
        this.caches.delete(minFreqKey)
      }
      this.caches.set(cache, {value: cache, freq: 1})
    }
  }
}
// test
var arr = [1,2,3,4,2,5,1,2,4,3]
const fifo = new LFUCache()
arr.forEach(item => fifo.set(item))
console.log(fifo.getCaches()); // 2,4,3

代码输出如下：

访问	in：1	in：2	in：3	in：4	in：2	in：5	in：1	in：2	in：4	in：3
存储	1(1)	1(1)	1(1)	2(1)	2(2)	2(2)	2(2)	2(3)	2(3)	2(3)
存储		2(1)	2(1)	3(1)	3(1)	4(1)	5(1)	5(1)	1(1)	4(1)
存储			3(1)	4(1)	4(1)	5(1)	1(1)	1(1)	4(1)	3(1)
命中	✗	✗	✗	✗	✓	✗	✗	✓	✗	✗

最久未使用：LRU

LRU 是 Least Recently Used 的缩写，LRU算法和OPT算法的理念有些类似，只不过一个分析的是现在，一个分析的是未来。LRU算法清除的是内存中最久没有被访问到的数据。它和数据被创建和最后访问更新的时间息息相关，这种算法算是命中率和使用频率非常高的一种。在vue的keey-alive组件中用的就是这种算法:keeyAlive

存在的问题：缓存污染，当存在偶发性、周期性的批量操作时，访问历史会被大量更新，造成后面的常规数据命中率急剧下降

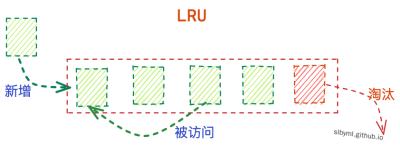
interface Icache {
  value: number
}
class LRUCache {
  private caches:Map<number,Icache >=new Map()
  private limit:number = 3
   getCaches():Map<number,Icache > {
    return this.caches
  }
  get(cache:number){ //数据被访问，就更新缓存
    if (this.caches.has(cache)) { // 存在即更新
      let temp = this.caches.get(cache);
      this.caches.delete(cache);
      this.caches.set(cache, {value:cache});
      return temp;
    }
    return -1;
  }
   set(cache:number):void {
    if (this.caches.has(cache)) {// 存在即更新（删除后加入）
      this.caches.delete(cache);
    } else if (this.caches.size >= this.limit) { // 缓存超过最大值，则移除最近没有使用的
      this.caches.delete(this.caches.keys().next().value);
    }
    this.caches.set(cache,{value:cache});
  }
}
// test
var arr = [1,2,3,4,2,5,1,2,4,3]
const fifo = new LRUCache()
arr.forEach(item => fifo.set(item))
console.log(fifo.getCaches()); //2、4、3

代码输出如下：

访问	in：1	in：2	in：3	in：4	in：2	in：5	in：1	in：2	in：4	in：3
存储	1	1	1	2	3	4	2	5	1	2
存储		2	2	3	4	2	5	1	2	4
存储			3	4	2	5	1	2	4	3
命中	✗	✗	✗	✗	✓	✗	✗	✓	✗	✗

优化LRU：LRU-K&Two queues(2Q)&MQ

很多业务中的最优算法都不是独立存在的，而是结合多种算法，继承他们的优点进行使用，LRU-K就是这样；其中K代表最近使用次数，我们可以认为上面的算法为LRU-1。此算法就是为了解决上面提到的“缓存污染”的问题，它的核心思想就是增加一个缓冲区：最近使用小于K次时进入缓冲队列，大于K次则进入LRUcache内。

2Q算法是LRU-2的一种具体实现，它的缓冲区规定使用FIFO来实现

• 优先从LRUcache中查找数据，如果命中则将数据取出来重新加入到LRUcache缓存末尾
• 当缓存穿透则在缓冲队列内查看是否命中
• 当缓冲队列内命中，则将该数据在队列内索引+1，否则将数据加入缓冲队列
• 当缓冲队列的索引达到了K，则将其从队列内删除并加入到LRUcache内
• 如果在插入时LRUcache已满，则按照LRU逻辑将最久未使用的数据置换掉，然后在插入到LRUcache末尾

具体代码实现可以结合上面算法来实现：FIFO(作为缓冲历史队列)+LRU(作为LRUcache)

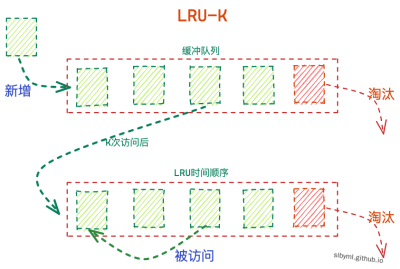
在实际环境中，K越大，命中率就越高，但却需要更多的访问才能将缓存记录替换掉，因此适用性可能并没有那么大，而LUR-2可能是综合各种因素后最优的选择，

当然还有更加进阶的LRU-Multi queues(MQ)算法，在LRU基础上增加了多个缓冲队列，是2Q的扩展，每个队列对应不同的优先级，根据淘汰算法进行相应的升级和降级处理，此算法复杂度相对较高、成本比较大

参考：

缓存淘汰算法（LFU、LRU、ARC、FIFO、2Q）分析、

LRU算法及其变种算法原理分析

操作系统原理：页置换算法

小红包免费领

小礼物走一走